Over the past decade, we’ve seen that Neural Networks can perform tremendously
well in structured data like images and text. Most of the popular models like
convolutional networks, recurrent, autoencoders work very well on data that have
a tabular format like a matrix or a vector. But what about unstructured data?
What about Graph data? Is there a model that can learn efficiently from them?
Probably you guessed it from the title. The answer is
Graph Neural Networks.
Graph Neural Networks were introduced back in 2005 (like all the other good
ideas) but they started to gain popularity in the last 5 years. The GNNs are
able to model the relationship between the nodes in a graph and produce a
numeric representation of it. The importance of GNNs is quite significant
because there are so many real-world data that can be represented as a graph.
Social networks, chemical compounds, maps, transportation systems to name a few.
So let’s find out the basic principles behind GNNs and why they work.
Let’s define our basic problem first: We want to map a given graph to a single
label, which can be a numeric value, a class or whatever really. In other
words:
And we want to find the function F. For example, imagine that each graph is a
chemical compound or a molecule and the label is the likelihood that this
molecule can be used to produce a certain drug. If we have a way to extract the
label from every graph, we essentially found a way to predict which molecules
are more likely to be used in a drug. Cool, right?
How do we do this? We already know a type of Neural Network that can be used on
Graphs (sort of). If you think about it, recurrent neural networks can operate
on a special type of graph. A chained graph (This a graph that is basically a
line). Time series are actually chained graphs, where each timestamp is a node
followed by the next timestamp.
So, in fact, we can build a network where each graph node is a recurrent unit
(LSTM or something else) and the information of the node is an embedding that
will be transferred through the chain (like a message). And because the units
are all recurrent, the information won’t be lost when the embedding travels
through the graph. It is our familiar Recurrent neural networks. Exactly the
same as the ones used in language translation and the other natural language
processing applications.
We can of course extend this idea to proper graphs and we get this:
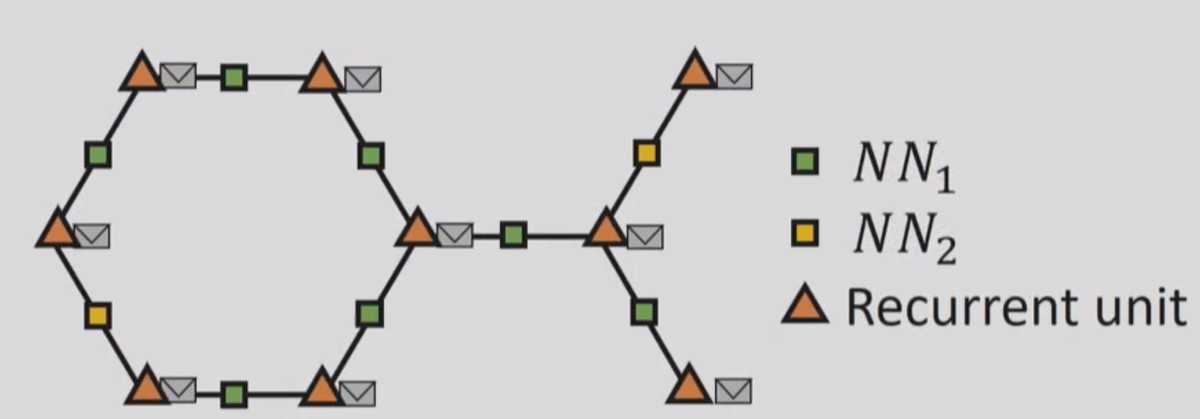
Graph neural networks: Variations and applications
This slide is taken from an awesome talk about GNNs by Microsoft
Research. Let’s see for a moment what is going on here.
Each orange triangle used to be graph node and it’s now replaced by a recurrent
unit. The envelopes represent the embeddings of the nodes that will travel
through the graph. Each graph edge is also replaced by a Neural network to
capture the information of the edge (its weight).
Now for the learning part. At a single time step, each node pulls the embedding
from all its neighbors, calculates their sum and passes them along with its
embedding to the recurrent unit, which will produce a new embedding. This new
embedding contains the information of the node plus the information of all the
neighbors. In the next time step, it will also contain the information of its
second-order neighbors. And so on and so on. The process continues until every
node knows about all the other nodes in the graph. Each one of the embeddings
has now information from all the other nodes. The final step is to collect all
embeddings and add them, which will give us a single embedding for the whole
graph.
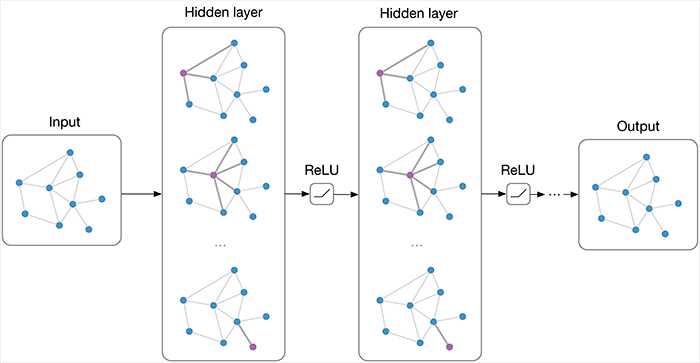
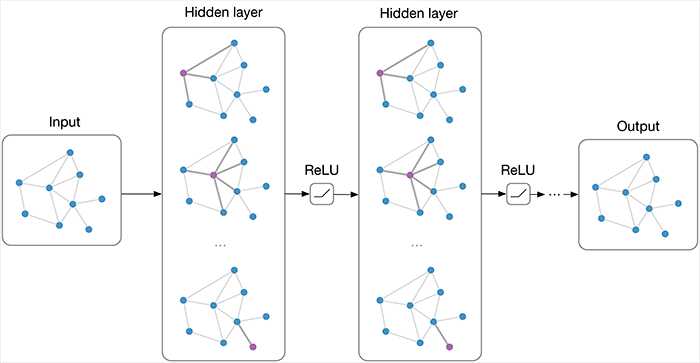
https://tkipf.github.io/graph-convolutional-networks/
That’s it. We did it. We manage to capture the whole graph in a single
embedding. This embedding can now be used in some other model to perform some
classification, prediction, clustering whatever. Let your imagination wander.
If you want to experiment with Graph Neural Networks, I got you covered:
I would personally go with the third one since it has better documentation but
is your choice.
Here you go. Ta-ra lad.
* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.