How Attention works in Deep Learning: understanding the attention mechanism in sequence models

I have always worked on computer vision applications. Honestly, transformers and attention-based methods were always the fancy things that I never spent the time to study. You know, maybe later and etc. Now they managed to reach state-of-the-art performance in ImageNet [3].

In NLP, transformers and attention have been utilized successfully in a plethora of tasks including reading comprehension, abstractive summarization, word completion, and others.

After a lot of reading and searching, I realized that it is crucial to understand how attention emerged from NLP and machine translation. This is what this article is all about. After this article, we will inspect the transformer model like a boss. I give you my word.

Let’s start from the beginning: What is attention? Glad you asked!

Memory is attention through time. ~ Alex Graves 2020 [1]

Always keep this in the back of your mind.

The attention mechanism emerged naturally from problems that deal with time-varying data (sequences). So, since we are dealing with “sequences”, let’s formulate the problem in terms of machine learning first. Attention became popular in the general task of dealing with sequences.

Sequence to sequence learning

Before attention and transformers, Sequence to Sequence (Seq2Seq) worked pretty much like this:

The elements of the sequence $x_1, x_2$

OK. So why do we use such models?

The goal is to transform an input sequence (source) to a new one (target).

The two sequences can be of the same or arbitrary length.

In case you are wondering, recurrent neural networks (RNNs) dominated this category of tasks. The reason is simple: we liked to treat sequences sequentially. Sounds obvious and optimal? Transformers proved us it’s not!

A high-level view of encoder and decoder

The encoder and decoder are nothing more than stacked RNN layers, such as LSTM’s. The encoder processes the input and produces one compact representation, called z, from all the input timesteps. It can be regarded as a compressed format of the input.

On the other hand, the decoder receives the context vector z and generates the output sequence. The most common application of Seq2seq is language translation. We can think of the input sequence as the representation of a sentence in English and the output as the same sentence in French.

In fact, RNN-based architectures used to work very well especially with LSTM and GRU components.

The problem? Only for small sequences (<20 timesteps). Visually:

Let’s inspect some of the reasons why this holds true.

The limitations of RNN’s

The intermediate representation z cannot encode information from all the input timesteps. This is commonly known as the bottleneck problem. The vector z needs to capture all the information about the source sentence.

In theory, mathematics indicate that this is possible. However in practice, how far we can see in the past (the so-called reference window) is finite. RNN’s tend to forget information from timesteps that are far behind.

Let’s see a concrete example. Imagine a sentence of 97 words:

“On offering to help the blind man, the man who then stole his car, had not, at that precise moment, had any evil intention, quite the contrary, what he did was nothing more than obey those feelings of generosity and altruism which, as everyone knows, are the two best traits of human nature and to be found in much more hardened criminals than this one, a simple car-thief without any hope of advancing in his profession, exploited by the real owners of this enterprise, for it is they who take advantage of the needs of the poor.” ~ Jose Saramago, “Blindness.”

Notice anything wrong? Hmmm… The bold words that facilitate the understanding are quite far!

In most cases, the vector z will be unable to compress the information of the early words as well as the 97th word.

Eventually, the system pays more attention to the last parts of the sequence. However, this is not usually the optimal way to approach a sequence task and it is not compatible with the way humans translate or even understand language.

Furthermore, the stacked RNN layer usually create the well-know vanishing gradient problem, as perfectly visualized in the distill article on RNN’s:

The stacked layers in RNN’s may result in the vanishing gradient problem. Source

Thus, let us move beyond the standard encoder-decoder RNN.

Attention to the rescue!

Attention was born in order to address these two things on the Seq2seq model. But how?

The core idea is that the context vector $z$ should have access to all parts of the input sequence instead of just the last one.

In other words, we need to form a direct connection with each timestamp.

This idea was originally proposed for computer vision. Larochelle and Hinton [5] proposed that by looking at different parts of the image (glimpses), we can learn to accumulate information about a shape and classify the image accordingly.

The same principle was later extended to sequences. We can look at all the different words at the same time and learn to “pay attention“ to the correct ones depending on the task at hand.

And behold. This is what we now call attention, which is simply a notion of memory, gained from attending at multiple inputs through time.

It is crucial in my humble opinion to understand the generality of this concept. To this end, we will cover all the different types that one can divide attention mechanisms.

Types of attention: implicit VS explicit

Before we continue with a concrete example of how attention is used on machine translation, let’s clarify one thing:

Very deep neural networks already learn a form of implicit attention [6].

Deep networks are very rich function approximators. So, without any further modification, they tend to ignore parts of the input and focus on others. For instance, when working on human pose estimation, the network will be more sensitive to the pixels of the human body. Here is an example of self-supervised approaches to videos:

Where activations tend to focus when trained in a self-supervised way. Image from Misra et al. ECCV 2016. Source

“Many activation units show a preference for human body parts and pose.” ~ Misra et al. 2016

One way to visualize implicit attention is by looking at the partial derivatives with respect to the input. In math, this is the Jacobian matrix, but it’s out of the scope of this article.

However, we have many reasons to enforce this idea of implicit attention. Attention is quite intuitive and interpretable to the human mind. Thus, by asking the network to ‘weigh’ its sensitivity to the input based on memory from previous inputs, we introduce explicit attention. From now on, we will refer to this as attention.

Types of attention: hard VS soft

Another distinction we tend to make is between hard and soft attention. In all the previous cases, we refer to attention that is parametrized by differentiable functions. For the record, this is termed as soft attention in the literature. Officially:

Soft attention means that the function varies smoothly over its domain and, as a result, it is differentiable.

Historically, we had another concept called hard attention.

An intuitive example: You can imagine a robot in a labyrinth that has to make a hard decision on which path to take, as indicated by the red dots.

A decision in the labyrinth. Source

In general, hard means that it can be described by discrete variables while soft attention is described by continuous variables. In other words, hard attention replaces a deterministic method with a stochastic sampling model.

In the next example, starting from a random location in the image tries to find the “important pixels” for classification. Roughly, the algorithm has to choose a direction to go inside the image, during training.

An example of hard attention.Source

Since hard attention is non-differentiable, we can’t use the standard gradient descent. That’s why we need to train them using Reinforcement Learning (RL) techniques such as policy gradients and the REINFORCE algorithm [6].

Nevertheless, the major issue with the REINFORCE algorithm and similar RL methods is that they have a high variance. To summarize:

Hard attention can be regarded as a switch mechanism to determine whether to attend to a region or not, which means that the function has many abrupt changes over its domain.

Ultimately, given that we already have all the sequence tokens available, we can relax the definition of hard attention. In this way, we have a smooth differentiable function that we can train end to end with our favorite backpropagation.

Let’s get back to our showcase to see it in action!

Attention in our encoder-decoder example

In the encoder-decoder RNN case, given previous state in the decoder as $\textbf{y}_{i-1}$

\textbf{e}_{i}=\operatorname{attention_{net}}\left(y_{i-1}, \textbf{h} \right) \in R{^n}

The index i indicates the prediction step. Essentially, we define a score between the hidden state of the decoder and all the hidden states of the encoder.

More specifically, for each hidden state (denoted by j) $\textbf{h}_1,\textbf{h}_2,\textbf{h}_n$

e_{i j}=\operatorname{attention_{net}}\left(\textbf{y}_{i-1}, h_{j}\right)

Visually, in our beloved example, we have something like this:

Notice anything strange?

I used the symbol e in the equation and α in the diagram! Why?

Because, we want some extra properties: a) to make it a probability distribution and b) to make the scores to be far from each other. The latter results in having more confident predictions and is nothing more than our well known softmax.

\alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)}

Finally, here is where the new magic will happen:

z_{i}=\sum_{j=1}^{T} \alpha_{i j} \textbf{h}_{j}

In theory, attention is defined as the weighted average of values. But this time, the weighting is a learned function! Intuitively, we can think of $\alpha_{i j}$

All the aforementioned are independent of how we choose to model attention! We will get down to that in a bit.

Attention as a trainable weight mean for machine translation

I find that the most intuitive way to understand attention in NLP tasks is to think of it as a (soft) alignment between words. But what does this alignment look like? Excellent question!

In machine translation, we can visualize the attention of a trained network using a heatmap such as below. Note that scores are computed dynamically.

Image by Neural Machine translation paper. Source

Notice what happens in the active non-diagonal elements. In the marked red area, the model learned to swap the order of words in translation. Also note that this is not a 1-1 relationship but a 1 to many, meaning that an output word is affected by more than one input word (each one with different importance).

How do we compute attention?

In our previous encoder-decoder example, we denoted attention as $\operatorname{attention_{net}}\left(y_{i-1}, \textbf{h} \right)$

While a small neural network is the most prominent approach, over the years there have been many different ideas to compute that score. The simplest one, as shown in Luong [7], computes attention as the dot product between the two states $y_{i-1}\textbf{h}$

In certain cases, the alignment is only affected by the position of the hidden state, which can be formulated using simply a softmax function $\operatorname{softmax}(y_{i-1},\textbf{h})$

The last one worth mentioning can be found in Graves A. [8] in the context of Neural Turing Machines and calculates attention as a cosine similarity $cosine[y_{i-1},\textbf{h}]$

To summarize the different techniques, I’ll borrow this table from Lillian Weng’s excellent article. The symbol $s_t$

Ways to compute attention. Source

The approach that stood the test of time, however, is the last one proposed by Bahdanau et al. [2]: They parametrize attention as a small fully connected neural network. And obviously, we can extend that to use more layers.

This effectively means that attention is now a set of trainable weights that can be tuned using our standard backpropagation algorithm.

As perfectly stated by Bahdanau et al. [2]:

“Intuitively, this implements a mechanism of attention in the decoder. The decoder decides parts of the source sentence to pay attention to. By letting the decoder have an attention mechanism, we relieve the encoder from the burden of having to encode all information in the source sentence into a fixed-length vector. With this new approach, the information can be spread throughout the sequence of annotations, which can be selectively retrieved by the decoder accordingly.” ~ Neural machine translation by jointly learning to align and translate

So, what do we lose? Hmm… I am glad you asked!

We sacrificed computational complexity. We have another neural network to train and we need to have $O(T^2)$

Quadratic complexity can often be a problem! Unless you own Google 😉

And that brings us to local attention.

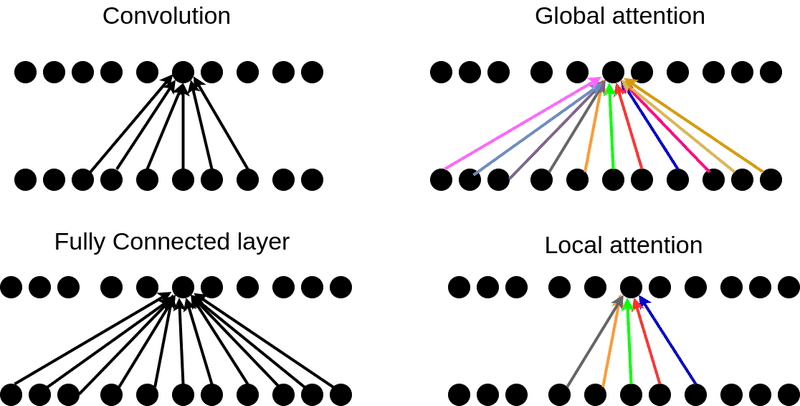
Global vs Local Attention

Until now we assumed that attention is computed over the entire input sequence (global attention). Despite its simplicity, it can be computationally expensive and sometimes unnecessary. As a result, there are papers that suggest local attention as a solution.

In local attention, we consider only a subset of the input units/tokens.

Evidently, this can sometimes be better for very long sequences. Local attention can also be merely seen as hard attention since we need to take a hard decision first, to exclude some input units.

Let’s wrap up the operations in a simple diagram:

The colors in the attention indicate that these weights are constantly changing while in convolution and fully connected layers they are slowly changing by gradient descent.

The last and undeniably the most famous category is self-attention.

Self-attention: the key component of the Transformer architecture

We can also define the attention of the same sequence, called self-attention. Instead of looking for an input-output sequence association/alignment, we are now looking for scores between the elements of the sequence, as depicted below:

Personally, I like to think of self-attention as a graph. Actually, it can be regarded as a (k-vertex) connected undirected weighted graph. Undirected indicates that the matrix is symmetric.

In maths we have: $\operatorname{self-attention_{net}}\left(x, x \right)$

Advantages of Attention

Admittedly, attention has a lot of reasons to be effective apart from tackling the bottleneck problem. First, it usually eliminates the vanishing gradient problem, as they provide direct connections between the encoder states and the decoder. Conceptually, they act similarly as skip connections in convolutional neural networks.

One other aspect that I’m personally very excited about is explainability. By inspecting the distribution of attention weights, we can gain insights into the behavior of the model, as well as to understand its limitations.

Think, for example, the English-to-French heatmap we showed before. I had an aha moment when I saw the swap of words in translation. Don’t tell me that it isn’t extremely useful.

Attention beyond language translation

Sequences are everywhere!

While transformers are definitely used for machine translation, they are often considered as general-purpose NLP models that are also effective on tasks like text generation, chatbots, text classification, etc. Just take a look at Google’s BERT or OpenAI’s GPT-3.

But we can also go beyond NLP. We briefly saw attention being used in image classification models, where we look at different parts of an image to solve a specific task. In fact, visual attention models recently outperformed the state of the art Imagenet model [3]. We also have seen examples in healthcare, recommender systems, and even on graph neural networks.

To summarize everything said so far in a nutshell, I would say: Attention is much more than transformers and transformers are more than NLP approaches.

Only time will prove me right or wrong!

Conclusion

For a more holistic approach on NLP approaches with attention models we recommend this Coursera course. So if you aim to understand transformers, now you are ready to go! This article was about seeing through the equations of attention.

Attention is a general mechanism that introduces the notion of memory. The memory is stored in the attention weights through time and it gives us an indication on where to look. Finally, we clarified all the possible distinctions of attention and showed a couple of famous ways to compute it.

As a next step, I would advise the TensorFlow tutorial on attention, which you can run in Google Colab. If you want to discover in more depth the principles of attention, the best resource is undeniably Alex Graves’ video from DeepMind:

If you reached this point, I guess you are super ready for our Transformer article.

Cited as:

@article{adaloglou2020normalization,

title = "How attention works in deep learning: understanding the attention mechanism in sequence models",

author = "Adaloglou, Nikolas and Karagiannakos, Sergios",

journal = "https://theaisummer.com/",

year = "2020",

url = "https://theaisummer.com/attention/"

}

Acknowledgements

Thanks to the awesome Reddit community for identifying my mistake. Memory is attention through time and not vice versa.

References

[1] DeepMind’s deep learning videos 2020 with UCL, Lecture: Attention and Memory in Deep Learning, Alex Graves
[2] Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.
[3][an image is worth 16×16 words: transformers for image recognition at scale](https://openreview.net/forum?id=YicbFdNTTy), Anonymous ICLR 2021 submission
[4] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).
[5] Larochelle H., Hinton G, (2010), Learning to combine foveal glimpses with a third-order Boltzmann machine
[6] Mnih V., Heess N., Graves A., Kavukcuoglu K., (2014), Recurrent Models of Visual Attention
[7] Luong M., Pham H , Manning C. D., (2015), Effective Approaches to Attention-based Neural Machine Translation
[8] Graves A., Wayne G. ,Danihelka I., (2014), Neural turing machines
[9] Weng L., (2018), Attention? Attention!, lilianweng.github.io/lil-log
[10] Stanford University School of Engineering, (2017), Lecture 10: Neural Machine Translation and Models with Attention

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.

Source link