This blog post presents an overview of classifier-free guidance (CFG) and recent advancements in CFG based on noise-dependent sampling schedules. The follow-up blog post will focus on new approaches that replace the unconditional model. As a small recap bonus, the appendix briefly introduces the role of attention and self-attention on Unets in the context of generative models. Visit our previous articles on self-attention and diffusion models for more introductory content on diffusion models and self-attention.
Introduction
Classifier-free guidance has received increasing attention lately, as it synthesizes images with highly sophisticated semantics that adhere closely to a condition, like a text prompt. Today, we are taking a deep dive down the rabbit hole of diffusion guidance. It all began when , in 2021, were looking for a way to trade off diversity for fidelity with diffusion models, a feature missing from the literature thus far. GANs had a straightforward way to accomplish this tradeoff, the so-called truncation trick, where the latent vector is sampled from a truncated normal distribution, yielding only higher likelihood samples in inference.
The same trick does not work for diffusion models as they rely on the noise to be Gaussian during training and inference. In search of an alternative, came up with the classifier guidance method, where an external classifier model is used to guide the diffusion model during inference. Shortly after, picked up on this idea and found a way of achieving the tradeoff without an explicit classifier, creating the classifier-free guidance (CFG) method. As these two methods lay the groundwork for all diffusion guidance methods that followed, we will spend some time getting a good grasp on these two before exploring the follow-up guidance methods that have developed since. If you feel in need of a refresher on diffusion basics, have a look at , available here.
Classifier guidance
Narrative: Dhariwal et al. are looking for a way to replicate the effects of the truncation trick for GANs: trading off diversity for image fidelity. They observed that generative models heavily use class labels when conditioned on them. Besides that, they explored other ideas to condition diffusion models on class labels and found an existing method that uses an external classifier
If we had training images without noise, would just be a supervised classifier trained on paired supervised data . However, diffusion models operate on noisy images at different timesteps . So, using standard classifiers trained on clean images does not work out of the box! Luckily, we can train a classifier on noisy images at different timesteps alongside the standard conditional diffusion model , enabling it to cope with all noise levels throughout the sampling process. To feed the classifier signal into the sampling process, we can leverage Bayes’ rule as follows. Consider the conditional distribution from which we want to sample.
where .
Recall that diffusion models generate samples by predicting the score function of the target distribution. The above formula gives us a way of obtaining a conditional score by combining the unconditional and classifier scores. The classifier score is obtained by taking the gradient of the classifier logits w.r.t. the noisy input at timestep . So far, the equation above for the conditional score is not very useful, yet it breaks down the conditional generation into two terms we can control in isolation. Now comes the trick:
where is a re-normalizing constant that is typically ignored. We have defined a new guided_score by adding a guidance weight to the classifier score term. This guidance weight effectively controls the sharpness of the distribution . With , we push the probability mass towards the modes of , e.g., we push a noisy picture of a dog to look more like the average dog.
Notice I am using the apostrophe to indicate that this is not precisely the conditional score function as it is up-weighted by . I am also using the subscript to show that this process is successive.
For , the equation leads to regular conditional generation, and for unconditional. Values between 0 and 1 give an interpolation of those signals. Sander Dieleman has made a beautiful 2-dimensional illustration of classifier guidance at
However, keep in mind that instead of 2 dimensions, images have height width three dimensions! It is not clear a priori that forcing the sampling process to follow the gradient signal of a classifier will improve image fidelity. Experiments, however, quickly confirm that the desired tradeoff occurs for sufficiently large guidance weights .
Limitations: In high noise scales, it is unlikely to get a meaningful signal from the noisy image, and taking the gradient of the noisy image tends to yield arbitrary and sometimes adversarial signals . Moreover, we need to train a classifier on noisy images in parallel with the training of the diffusion models.
Classifier-free guidance
Narrative: The aim of classifier-free guidance is simple: To achieve an analogous tradeoff as classifier guidance does, without the need to train an external classifier. This is achieved by employing a formula inspired by applying the Bayes rule to the classifier guidance equation. While there are no theoretical or experimental guarantees that this works, it often achieves a similar tradeoff as classifier guidance in practice.
TL;DR: A diffusion sampling method that randomly drops the condition during training and linearly combines the condition and unconditional output during sampling at each timestep, typically by extrapolation.
The first step is to solve the guidance equation:
for the explicit conditioning term:
The conditioning term is thus a linear function of the conditional and unconditional scores. Crucially, both scores can be taken from diffusion model training. This avoids training a classifier on noisy images, yet it creates another problem: we now have to train 2 diffusion models: conditional and unconditional. To get around this, the authors propose the simplest possible thing: train a conditional diffusion model , with conditioning dropout. During the training of the diffusion model, we ignore the condition with some probability . Typically, %. Diffusion models behave by design differently to the timestep . We can now use
In our new-old formula from classifier guidance:
In this formulation, acts as the gradient of the implicit classifier, producing images that follow the condition. We have essentially constructed the “noisy classifier’” from our generative model. Conditional diffusion models are secretly classifiers , but that’s for another day. CFG offers an interesting trade-off for : It aligns the noisy image to follow the conditioning signal in contrast to the unconditional score.
Same as in classifier-based guidance, CFG leads to “easy to classify”, but often at significant cost to diversity (by sharpening ). We will extensively dive into the CFG tradeoff while reviewing different follow-up papers. Below is what the curve looks like on ImageNet regarding quality, as measured by the inception score (IS) versus the frechet inception distance (FID).
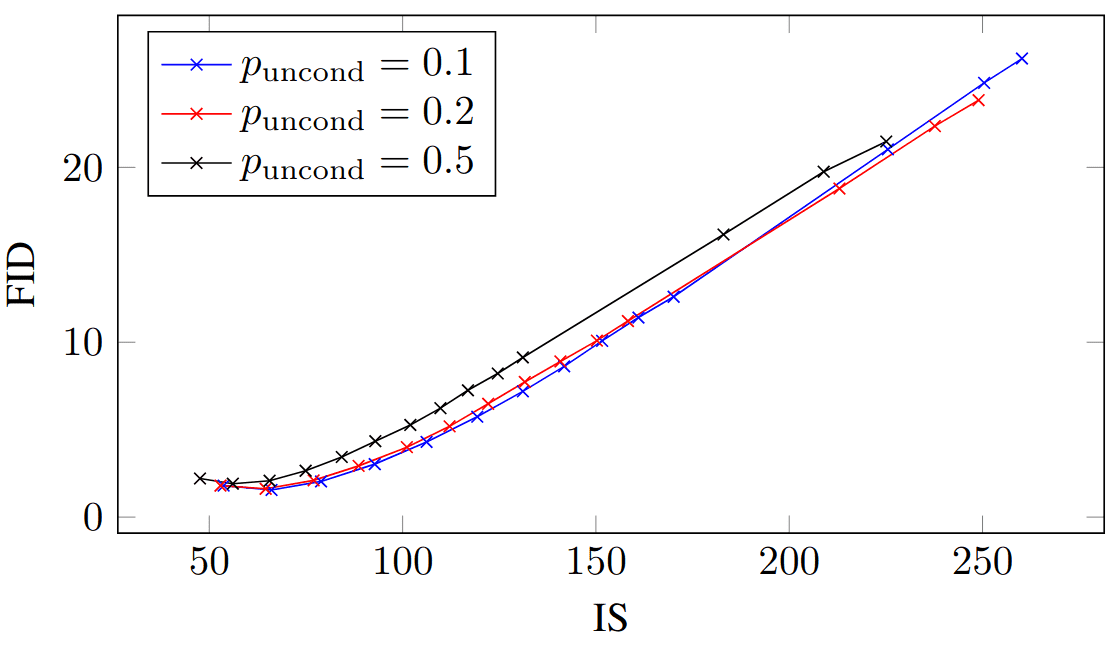
IS/FID curves over guidance strengths for ImageNet 64×64 models. Each curve represents a model with unconditional training probability . The figure is taken from Jonathan Ho and Tim Salimans . No changes were made.
Interleaved linear correction: An essential aspect of CFG is that it’s a linear operation in the high-dimensional image space, applied iteratively in each time step . CFG is interleaved with a non-linear operation, the diffusion model (i.e. a Unet). So, one magical aspect is that we apply a linear operation on the timestep, but it has a profound non-linear effect on the generated image. From this perspective, all guidance methods try to linearly correct the denoised image at the current timestep, ideally repairing visual inconsistencies, such as a dog with a single eye.
Fun fact: The CFG paper was initially submitted and rejected in ICLR 2022 by the title Unconditional Diffusion Guidance. Here is what the AC comments:
“However, the reviewers do not consider the modification to be that significant in practice, as it still requires label guidance and also increases the computational complexity.”
Limitations of CFG
There are three main concerns with CFG: a) intensity oversaturation, b) out-of-distribution samples for very large weights and likely unrealistic images, and c) limited diversity from easy-to-generate samples like simplistic backgrounds. In , the authors discover that CFG with separately trained conditional and unconditional models does not always work as expected. So, there is still much to understand about its intricacies.
An alternative formulation of CFG
Some papers use a different but mathematically identical formulation CFG. To see that they describe the same equation, here is the derivation ():
The guidance term is the same as above; the only difference is the weight . This formulation emphasizes the use of CFG for extrapolation, as all weights correspond to extrapolation, which is CFG’s predominant use case.
Static and dynamic thresholding for CFG
Narrative: Static and dynamic thresholding is a simple and naive intensity-based solution to the issues arising from CFG, like oversaturated images.
TL;DR: A linear rescaling on the intensities of the denoised image during CFG-based sampling, either without clipping (static) or with clipping (dynamic) the intensity range.
A large CFG guidance weight improves image-condition alignment but damages image fidelity . High guidance weights tend to produce highly saturated. The authors find this is due to a training-sampling mismatch from high guidance weights. Image generative models like GANs and diffusion models take an image in the range of integers [0,255] and normalize it to [-1,1]. The authors empirically find that high guidance weights cause the denoised image to exceed these bounds since we only drop the condition with some probability during training. This means that the diffusion model is trained conditionally or unconditionally during training. CFG is applied iteratively for all timesteps, leading to unnatural images, mainly characterized by high saturation.
Static thresholding refers to rescaling the intensity values of the denoised image back to [-1,1] after each step. Nonetheless, static thresholding still partially mitigates the problem and is less effective for large weights. Dynamic thresholding introduces a timestep-dependent hyperparameter . The pixel values are first clipped to and subsequently rescaled back to [-1,1] by dividing by . Hence, dynamic thresholding is the same as static thresholding but clips a portion of extreme brightness values before rescaling. At each sampling step, is set to a certain percentile absolute pixel value. In this way, one can adaptively adjust the scaling to the statistics of the image at this timestep. Below, the authors visualize the impact of thresholding.
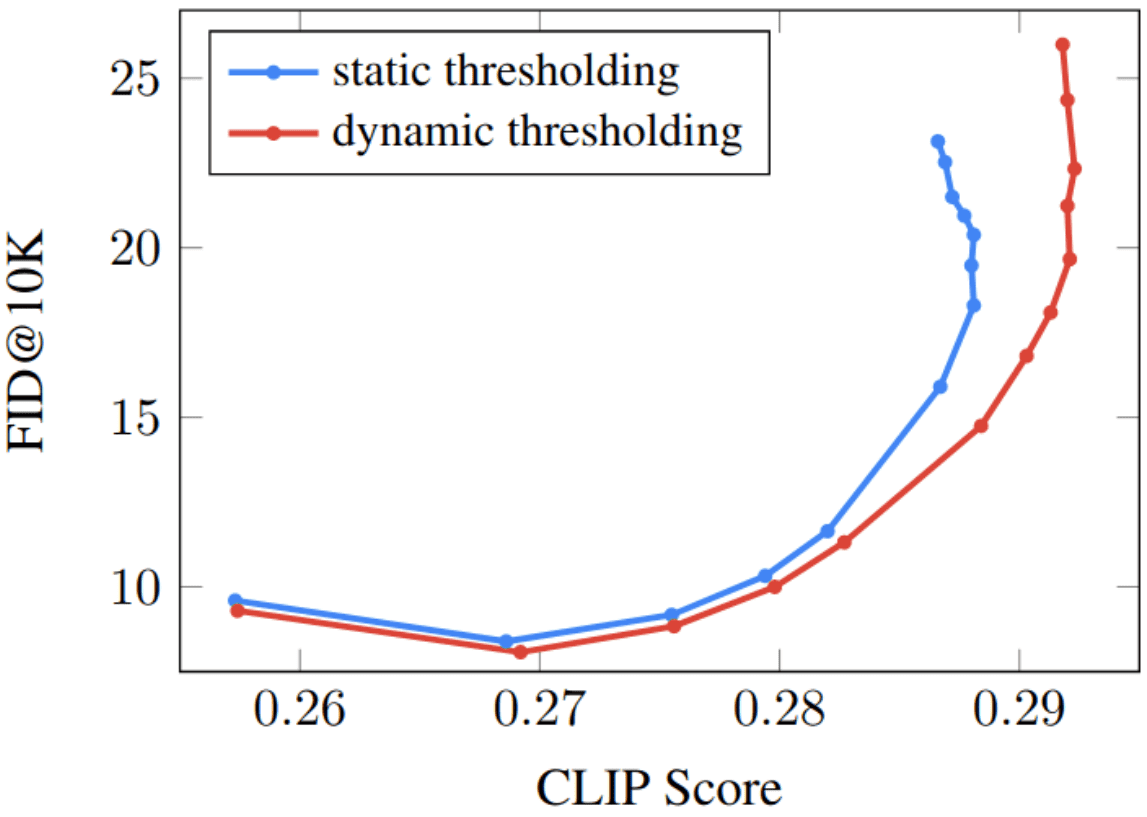
Pareto curves that illustrate the impact of thresholding by sweeping over w=[1, 1.25, 1.5, 1.75, 2, 3, 4, 5, 6, 7, 8, 9, 10]. The figure is taken from ImageGen . No changes were made.
The authors adaptively decide the value of for each timestep to be the intensity percentile . Due to the range clamping, dynamic thresholding prevents saturation at each step by pushing pixel intensities near -1 and 1 inwards .

Static vs. dynamic thresholding on non-cherry picked 256 × 256 samples using a guidance weight of 5, using the same random seed. The text prompt used for these samples is “A photo of an astronaut riding a horse.” When using high guidance weights, static thresholding often leads to oversaturated samples, while dynamic thresholding yields more natural-looking images. The snapshot is taken from the appendix of the ImageGen paper . CLIP score is a measure of image-text similarity used for text-to-image models. The CLIP score measures the similarity between the generated image and the input text prompt. No changes were made.
Improving CFG with noise-dependent sampling schedules
Condition-annealing diffusion sampler (CADS)
Narrative: Sadat et al. was one of the first papers to explore non-constant weights in CFG. They noticed that even a simple linear schedule that interpolates between unconditional and conditional generation increases diversity. They saw additional improvements by adjusting the strength of the condition rather than the weight itself.
TL;DR: A diffusion sampling variation of CFG that adds noise in the conditioning signal, targeting to increase diversity. The noise is linearly decreased during sampling; inversely, the conditioning signal is annealed.
Dynamic CFG baseline
In , the authors create a CFG-based baseline by making the guidance weight dependent on the noise scale . Noise-dependent is equivalent to time-dependent and is used interchangeably. At the beginning of the sampling process, we have and as , we are in the low noise region . Within this range, one can define a sub-range of where the sampling procedure linearly shifts from unconditional to conditional via linear interpolation. This results in a noise dependent weight such that
where is following a piecewise linear schedule, where
The authors provide preliminary results using the so-called Dynamic CFG, which show a decrease in FID.
CADS
First, CADS is a modification of CFG and not a standalone method. CADS employs an annealing strategy on the condition . It gradually reduces the amount of corruption as the inference progresses. More specifically, similar to the forward process of diffusion models, the condition is corrupted by adding Gaussian noise based on the initial noise scale
The schedule is the same as the previous baseline following the pattern: fully corrupted condition (gaussian noise) partially corrupted condition (increasing linearly) uncorrupted conditional.
Rescaling the conditioning signal Adding noise alters the mean and standard deviation of the conditioning vector. To revert this effect, the authors rescale the conditioning vector such that:
where is another hyperparameter . Rescaling serves as a regularizer and helps prevent divergence, especially when the noise scale is high . This leads us to:
In summary, CADS modulates (via noise-dependent Gaussian noise) instead of simply applying a schedule to the guidance scale . Interestingly, the diffusion model has never seen a noisy condition during training, which makes it applicable to any conditionally trained diffusion model.
Limited interval CFG
Narrative: Kynkaanniemi et al. took the idea of weak guidance early and stronger guidance later and distilled it into a simple and elegant method. Unlike concurrent works, they identified that the schedule does not need to increase monotonically. They do not try to modify the condition as in CADS and focus on the guidance weight. Using a toy example, they observe that applying guidance at all noise levels causes the sampling trajectories to drift quite far from the data distribution. This is caused because the unconditional trajectories effectively repel the CFG-guided trajectories, mainly during high noise levels. On the other hand, applying CFG at low noise levels on class-conditional models has small to no effect and can be dropped.
TL;DR: Apply CFG only in the intermediate steps of the denoising procedure, effectively disabling CFG at the beginning and end of sampling, practically setting to 0 (conditional only denoising).}
One of the most simple and powerful ideas has been recently proposed by Kynkaanniemi et al. . The authors show that guidance is harmful during the first sampling steps (high noise levels) and unnecessary toward the last inference steps (low noise levels). They thus identify an intermediate noise interval for two state-of-the-art class conditional models on ImageNet, namely EDM2 and DiT . The hyperparameters and ) are picked based on FID evaluation. This is a widespread trend in generative models worth mentioning here. As training becomes prohibitively expensive, the community attempts to move hyperparameter selection in the sampling stage.} In practice, using the equation based on :
the authors set to be noise dependent such that and only apply it in an intermediate interval. This strategy disables CFG at the beginning and at the end of the sampling process

Quantitative results on ImageNet-512. Limiting the CFG to an interval improves both FID and significantly without altering the model complexity. The sampling cost is a bit lower due to fewer guidance evaluations. Baseline models are EDM2 and DiT . The table snapshot has been taken from .
Intriguingly, the hyperparameter choice varies based on the metric used to quantify image fidelity and diversity. is a new metric that replaces the supervised learned features of InceptionV3 with DINOv2 . favors higher noise intervals and larger guidance weights. It has been previously stated that favors images with better global coherency , which frequently aligns with higher perceptual quality as judged by humans. In both guidance methods (naive CFG and interval CFG), prefers higher guidance strength than FID, as illustrated below. We note that FID is more sensitive to (invisible) small shifts in image statistics.
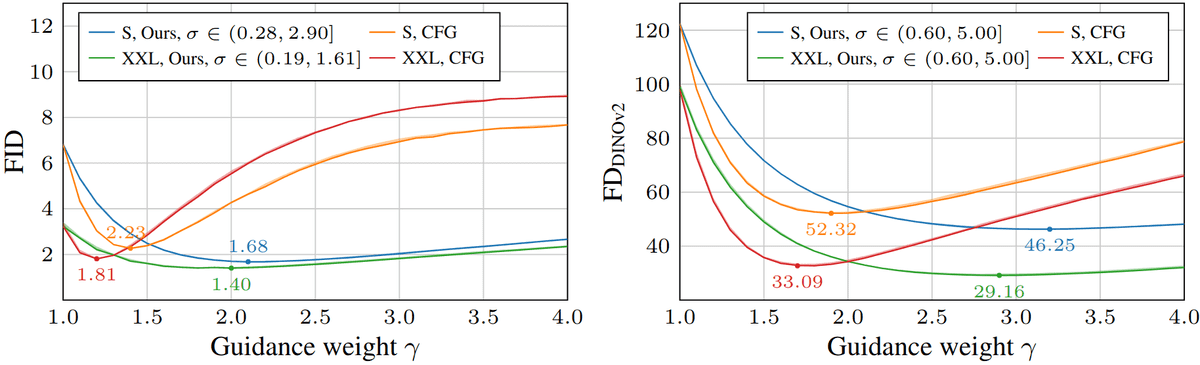
FID and as a function of guidance weight for classifier-free guidance (orange, red) and our method where the guidance has been limited to the stated interval (blue, green). The image is taken from . No changes were made.
Analysis of Classifier-Free Guidance Weight Schedulers
TL;DR: Another concurrent experimental study centered around text-to-image diffusion models was conducted by Wang et al.. They demonstrate that CFG-based guidance at the beginning of the denoising process is harmful, corroborating with . Instead of disabling guidance, Wang et al. use monotonically increasing guidance schedules based on a large-scale ablation study. Linearly increasing the guidance scale often improves the results over a fixed guidance value on text-to-image models without any computational overhead.
There are probably nuanced differences in how guidance works in class-conditional and text-to-image models, so insights do not always translate to one another. While apply the guidance in a fixed interval for text-to-image models and use a simple linear schedule, it’s hard to deduce the best approach. We highlight that a monotonical schedule requires less hyperparameter search and seems easier to adopt for future practitioners in this space. While both works compare with vanilla CFG, the real test would be a human evaluation using all three methods and various state-of-the-art diffusion models.
Rethinking the Spatial Inconsistency in Classifier-Free Diffusion Guidance
Narrative: Previous works applied noise-dependent guidance scales to improve diversity and the overall visual quality of the distribution of the produced samples. This work focused on improving spatial inconsistencies within an image for text-to-image diffusion models like Stable Diffusion. It is argued that spatial inconsistencies in text-to-image models come from applying the same guidance scale to the whole image.
TL;DR Leverage attention maps to get an on-the-fly segmentation map per image to guide CFG differently for each region of the segmentation map. Here, regions correspond to the different tokens in the text prompt. Visit the appendix first to understand self- and cross-attention maps in this context.
Shen et al. argue that a guidance scale for the whole image results in spatial inconsistencies since different regions in the latent image have varying semantic strengths, focused on text-to-image diffusion. The overall premise of this paper is the following:
-
Find an unsupervised segmentation map (per token in the text prompt) based on the internal representation of self- and cross-attention (see Appendix).
-
Refine the segmentation maps to make the object boundaries clearer and remove internal holes.
-
Use the segmentation maps to scale the guided CFG score to equalize the varying guidance scale per semantic region .
where is an element-wise product known as Hadamrd product.
To get a segmentation map on the noisy image , a set of binary masked regions, based on the token (words) prompts, is defined as where . To this end, the cross-attention maps,
from the last two layers and heads (from the smallest two resolutions of the Unet encoder) are upsampled and aggregated () via averaging (second column in Fig.). Then, the cross-attention maps are refined by multiplying each one with the corresponding self-attention maps at each attention layer. Instead of simply multiplying the self-attention map (third column in Fig.), they incorporate the idea of feature propagation from graphs:
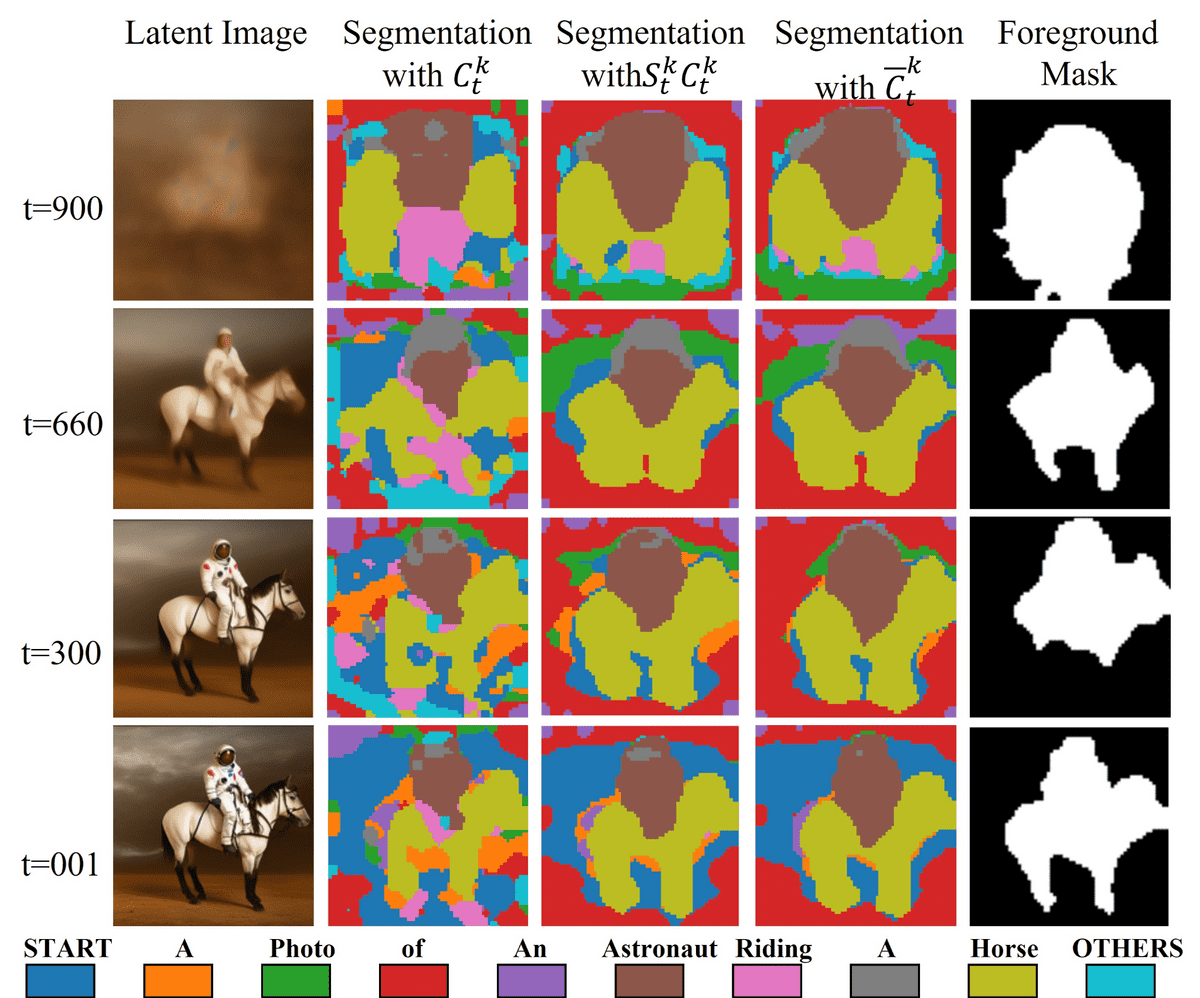
First column: predicted image at timestep . Second column: segmentation map from cross-attention only (). Third column: multiplying with self-attention map . Fourth column: Graph-like propagation for Q=4. Regions labeled by different colors correspond to different tokens. The last column combines the binary mask of the token “astronaut” and “horse”. The image is taken from , licensed under CC BY 4.0. No changes were made.
The result is shown in the fourth column in the above figure . Here, can be interpreted as an adjacency matrix among patches and as the graph signal (feature matrix). Each element of is non-negative, and the sum of each row is equal to one due to softmax. This method can be seen as an extension of a graph convolution operation where higher-order neighbors are considered. corresponds to the self-attention matrix raised to the power of , capturing -hop neighbors. Higher powers incorporate information from further neighbors in the adjacency matrix. Subsequently, all attention maps are spatially normalized and the operation is applied on the token dimension ():
Based on , the corresponding region masks can be derived by binarizing the refined attention map . The final per is interpolated and reshaped to the same size as , and the masks are weighted to get the final scale mask . To the best of our understanding, the output is copied three times to match the three image channels. Using the prompt “a photo of an astronaut riding a horse”, one must combine the binary masks from the words “astronaut” and horse “horse” to create a foreground mask. The authors additionally define a hand-crafted way to define , but we leave it outside this overview.
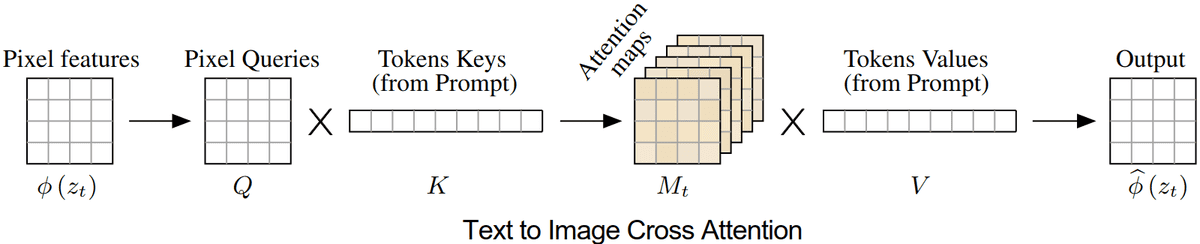
Cross-attention in Unet diffusion models. Visual and textual embedding are fused using cross-attention layers that produce spatial attention maps for each textual token. Critically, keys and values come from the condition (text prompt). Snapshot is taken from Hertz et al. . No changes were made.
How cross-attention works. Previous studies provide intuition on the impact of the attention maps on the model’s output images. To start, here is how the cross-attention operation as it is implemented in Unets at each timestep .
for query , key , value at timestep , where , are to the downsampled height and width. The scalar is the channel dimension of the encoder module of Unet that must match the text embedding dimension for each token. Tokens are word embeddings in this case; thus, we have tokens in total.
where . In Cross-attention, the condition is injected into the visual features on Unets, which typically happens near the bottleneck dimension of the encoder. It can also be applied in multiple encoder blocks. Intuitively, the cross-attention map allows the diffusion model to bind the text tokens in specific image regions . The cross-attention map is known to contain (global) structural information. This occurs in the first matrix multiplication of the keys with the condition with the visual query . In the figure below, the authors keep the attention maps from the prompt “lemon cake” () and swap based on various prompts. Fixing the generated attention maps to “lemon cake” (using the same random noise/seed) gives the generated cakes an identical global structure. You can see the control group at the bottom of the figure when using the prompt for both and .

The figure is taken from Hertz et al. . No changes were made.
Condition swap in cross-attention. In , the authors show the impact of changing the condition during inference for text-to-image models. From left to right in the figure below, the five images are produced with different transition percentages: 0%, 7%, 30%, 60%, and 100%. In the last steps of denoising, the condition has no visual impact. Switching condition after 40% of the denoising overwrites the imprint of the initial condition.
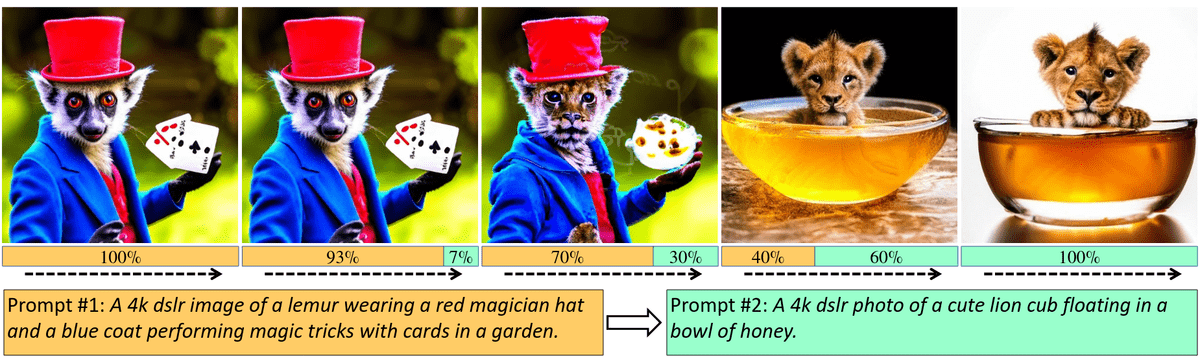
Visualizing the effect of prompt switching during diffusion sampling. Second column: in the last steps of denoising, the text inputs have negligible visual impact, indicating that the text prompt is not used. Third column: the 70-30 ratio leaves imprints in the image from both prompts. Fourth column: the first 40% of denoising is overridden from the second prompt. The denoiser utilizes prompts differently at each noise scale. The snapshot is taken from , licensed under CC BY 4.0. No changes were made
Self-attention vs cross-attention. However, the cross-attention module in the Unet should be distinct from the self-attention module. We have identified that the cross-attention module only exists in text-to-image diffusion Unets, while the self-attention component also exists in class conditional and unconditional diffusion models. So even though we tend to represent with the condition in both cases, class condition, and test prompts are processed differently under the hood. Here is how self-attention is computed in a Unet, for query , key , value at timestep , where , are to the downsampled height and width, while is channel dimensions at this encoder module.
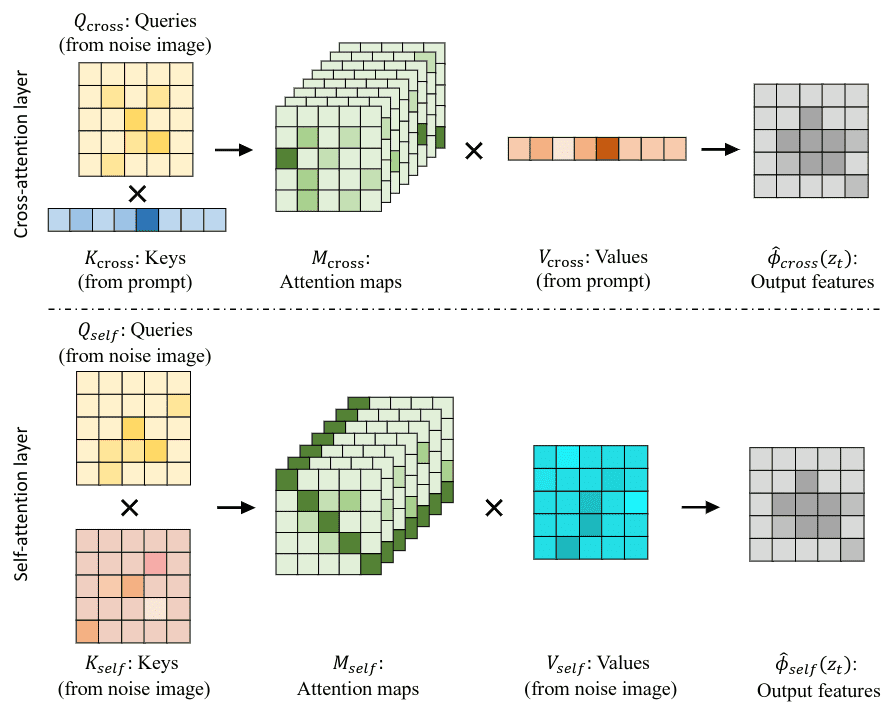
Cross and self-attention layers in Unet denoisers such as Stable Diffusion. The image is taken from , licensed under CC BY 4.0. No changes were made.
Liu et al. conducted a large-scale experimental analysis on Stable diffusion, focused on image editing. The authors demonstrate that cross-attention maps in Stable Diffusion often contain object attribution information. On the other hand, self-attention maps play a crucial role in preserving the geometric and shape details. The pair comes from the same image during image synthesis and the source/reference image for image editing.
Conclusion
We have presented an overview of CFG and its schedule-based sampling variants. In short, monotonically increasing schedules are beneficial, especially for text-to-image diffusion models. Alternatively, using CFG only in an intermediate interval reaps all the desired benefits without oversacrificing diversity while keeping the computation budget lower than CFG. Finally, the self and cross-attention modules of diffusion Unets provide useful information that can be leveraged during sampling, as we will see in the next one. The next article will investigate CFG-like approaches that try to replace the unconditional model, in an effort to make CFG a more generalized framework. For a more introductory course, we highly reccomnd the Image Generation Course from Coursera.
If you want to support us, share this article on your favorite social media or subscribe to our newsletter.
Citation
@article{adaloglou2024cfg,
title = "An overview of classifier-free guidance for diffusion models",
author = "Adaloglou, Nikolas, Kaiser, Tim",
journal = "theaisummer.com",
year = "2024",
url = "https://theaisummer.com/classifier-free-guidance"
}
Disclaimer
Figures and tables shown in this work are provided based on arXiv preprints or published versions when available, with appropriate attribution to the respective works. Where the original works are available under a Creative Commons Attribution (CC BY 4.0) license, the reuse of figures and tables is explicitly permitted with proper attribution. For works without explicit licensing information, permissions have been requested from the authors, and any use falls under fair use consideration, aiming to support academic review and educational purposes. The use of any third-party materials is consistent with scholarly standards of proper citation and acknowledgment of sources.
References
* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.



